Sonnenteleskope
H-alpha Sonnenteleskope ermöglichen die Beobachtung von Strukturen der Sonne, die im Licht der Wellenlänge des angeregten Wasserstoffs bei 656,28nm Wellenlänge strahlen. Diese H-alpha Linie (Wellenlänge) ist die Wasserstofflinie mit der grössten Strahlungsintensität auf der Sonne. Sie zeigt sehr schön die Sonnenflecken, Fackeln, Filamente, Flares und die Protuberanzen am Sonnerand.
Diese Details der Sonnenstruktur treten umso deutlicher zum Vorschein, je enger die Bandbreite des eingesetzten H-alpha Filters ist. Die Bandbreite solcher H-alpha Filter reicht von etwa 1 Ängström bis hinunter zu 0,3 Ängström. 1 Ängström entspricht 0,1nm.
Zum Erzeugen solch enger Bandbreiten werden sogenannte Etalon-Filter eingesetzt. Ein Etalon-Filter arbeitet nach dem Prinzip des Fabry-Perot-Interferometers. Es besteht aus zwei teildurchlässigen Spiegeln die in definiertem Abstand zueinander, hochgenau positioniert sein müssen.
Die beiden sich gegenüber liegenden Spiegel wirken als optischer Resonator, d.h. das eintretende Licht wird zwischen Ihnen hin und her reflektiert und interferiert dabei. Je nach Phasenlage und Wellenlänge löschen sich die Lichtwellenfronten aus oder interferieren konstruktiv, d.h. die Lichtintensitäten addieren sich.
Diese konstruktive Interferenz tritt nur für Lichtwellenlängen auf, die die Resonanzbedingung des optischen Resonators erfüllen, d.h. es entstehen sehr schmalbandige Maxima, die periodisch im Spektrum auftreten. Der Abstand dieser Maxima wird durch den Spiegelabstand bestimmt.
Die Bandbreite des einzelnen Maximums wird durch die Anzahl der interferierenden Strahlenbündel bestimmt. Je grösser die Anzahl der interferierenden Strahlenbündel desto schärfer werden die Maxima im Spektrum begrenzt, d.h. desto enger wird die Bandbreite.
Die Anzahl der interferierenden Strahlenbündel und somit die Bandbreite der Maxima ist umso grösser, je geringer die Dämpfung im Resonator ist. D.h. je höher die Reflektivität der Spiegelbeschichtung, desto enger die Bandbreite der erzeugten Maxima.
Um solch ein Fabry-Perot-Etalon für die Sonnenbeobachtung in H-alpha nutzen zu können muss ein Maximum der Transmission des Filters genau auf der Wellenlänge der H-alpha Linie liegen und nur dieses Maximum darf beobachtet, d.h. zum Ausgang des Sonnenteleskops übertragen werden.
Die Übertragung von genau einem Maximum erreicht man durch den Einsatz eines Blockfilters. Das Blockfilter wird im Strahlengang hinter dem Etalon-Filter positioniert. Es besitzt eine Bandbreite von wenigen Nanometern um die H-alpha Linie.
Um die maximale Bandbreite des Blockfilters zu bestimmen, muss man die an Etalon-Sonnenfiltern vorhandene Tuningmöglichkeit mit einbeziehen. Tuning heisst in diesem Fall eine feine Verschiebung der Durchlasskurve des Filters in beiden Richtungen des Spektrums. Eine Verschiebung der Durchlasskurve wird durch die Veränderung des Spiegelabstands im Resonator erreicht.
Bei Etalon-Sonnenfiltern wird die Verschiebung der Durchlasskurve entweder durch die Lagerung des Filters in einer Kippfassung, durch ein genaues Beheizen des Filters oder durch Druckluftsysteme realisiert. Diese Verstellmöglichkeit ist notwendig, weil sich die Filterparameter durch Umgebungseinflüsse wie Temperaturschwankungen oder Luftdruckschwankungen ändern und sich dadurch die spektrale Durchlasskurve des Filters verschiebt.
Um die sehr engen Bandbreiten von Etalon-Filtern messen zu können sind uns lediglich zwei Möglichkeiten bekannt. Eine Möglichkeit ist der Einsatz eines weiteren Etalon-Filters, bei dem der Abstand der beiden Spiegel in extrem kleinen Schritten verändert werden kann.
Solche SFPI (Scanning-Fabry-Perot-Interferometer) werden zur Messung der Spektren von schmalbandigen Lasern eingesetzt. Die geringe Veränderung des Abstandes der Spiegel wird durch den Einsatz von Piezoelementen erreicht. Um die Empfindlichkeit des Filters gegenüber einem eventuellen Winkelversatz des eintretenden Lichtstrahls zu minimieren, werden Spiegel eingesetzt deren Vorder- und Rückseiten die gleiche, konkave Krümmung besitzen.
Zur sicheren Messung der Bandbreite von Etalon-Sonnenfiltern muss die Bandbreite der SFPI um den Faktor 5 geringer sein. Beim Scannen erhält man dann 10 Messwerte der spektralen Druchlasskurve des Sonnenfilters.
Solch extrem enge Bandbreiten von SFPI werden erreicht, indem man den Abstand der Spiegel vergrössert und die Spiegelflächen entsprechend beschichtet.
Die Vorderseite der Spiegel wird dazu dielektrisch, hochreflektiv verspiegelt um die Dämpfung im Resonator so klein wie möglich zu halten. Die Rückseiten werden vergütet um Transmissionsverluste beim Strahl Ein- und Austritt zu minimieren.
Da man beim Messen von Laserspektren mit hohen Lichtintensitäten arbeiten kann, es aber am Ausgang von Etalon-Sonnenteleskopen unter Laborbeleuchtung zu recht bescheidenen Lichtintensitäten kommt, haben wir uns gegen den Bau eines solchen Filters zur spektralen Messung an Etalon-Sonnenfiltern entschieden.
Die zweite Möglichkeit zur Bandbreitenbestimmung von Etalon-Sonnenfiltern ist der Einsatz von Gitterspektrometern. Handelsübliche, erschwingliche Gitterspektrometer besitzen spektrale Auflösungen im Nanometerbereich und messen über grosse Wellenlängenbereiche. Das von uns für Reflexionsmessungen eingesetzte Gitterspektrometer besitzt z.B. eine spektrale Auflösung von 2nm und misst über einen Wellenlängenbereich von 200-1200nm.
Um ein Gitterspektrometer für unseren Zweck einsetzen zu können, muss es entsprechend modifiziert werden. Als gute Basis haben wir dazu ein Spektrometer der kanadischen Firma Aseq-Instruments gewählt. Aseq bietet von Haus aus eine individuelle Anpassung der Spektrometer an die Messaufgabe.
Das für Aseq maximal Machbare für unsere Messungen war ein Gitterspektrometer in symmetrischer Czerny-Turner Konfiguration und einem holographischen Beugungsgitter mit 2400 Linien pro Millimeter. Die Grösse des Eingangspalt war 25 Mikrometer und die Brennweite der beiden Spiegel 150 Millimeter.
Symmetrisch bedeutet hier, dass die Brennweite des Kollimationsspiegels und die Brennweite des Fokussierspiegels gleich gross sind, was bedeutet, dass der Eingangsspalt in Originalgrösse auf dem Detektor abgebildet wird.
Als Detektor wird ein lineares CCD-Zeilenarray mit 3648 Pixeln eingesetzt, dass luftdicht mit 2 Peltierelementen eingegossen wurde. Durch diese intensive Peltierkühlung der Detektorelemente wird deren Dunkelstrom extrem reduziert. So ist ein enorm gutes Signal-Rausch-Verhältnis möglich, wodurch auch sehr schwache Strahlung sicher detektiert werden kann. Das einzelne Detektorelement des CCD-Zeilenarrays ist rechteckig, 8 Mikrometer breit und 200 Mikrometer hoch. Bei 3648 Detektorelementen entspricht das einer Detektorbreite von 29,1 Millimetern.
Die spektrale Auflösung der beschriebenen Originalkonfiguration lässt sich mit 2 Gleichungen berechnen: Die reziproke, lineare Dispersion der Anordung wird mit Hilfe der Gleichung RLD=GK*cos(Beta)/fFOK berechnet.
GK ist die Gitterkonstante von 1/2400mm, Beta ist, wie in der beispielhaften Abbildung zum Czerny-Turner Aufbau zu sehen, der Winkel zwischen der Gitternormalen und der ersten Beugungsordnung der Zentralwellenlänge und fFOK ist die Brennweite des Spiegels, der die Wellenlängenbereiche auf den Detektor fokussiert.
Czerny-Turner Aufbau
Die RLD berechnet sich dann zu 1,389nm/mm. Das bedeutet auf 1mm Detektorlänge werden 1,389nm spektrale Bandbreite abgebildet. Mit Hilfe der RLD und der Detektorbreite lässt sich die maximal abbildbare Bandbreite des Spektrometers berechnen: Bandbreite=RLD*Detektorbreite.
In Originalkonfiguration lassen sich also 40,42nm Bandbreite des Spektrum abbilden. Teilt man die Bandbreite durch die Anzahl der Detektorelemete, 40,42nm/3648 erhält man die spektrale Bandbreite pro Detektorelement, also 0,011nm, was 0,11Ängström pro Detektorelement (Pixel) entspricht.
Durch gleiche Brennweiten der beiden Spiegel wird der Eingangsspalt (theoretisch) in Originalgrösse auf den Detektorelementen abgebildet. Bei 25 Mikrometern Spaltbreite liegt der Spalt über 25/8 = 3,125 Detektorelementen. 3,125 Detektorelemente * 0,011nm Bandbreite pro Detektorelement ergibt eine theoretische optische Auflösung von 0,034 nm, was 0,34 Ängström entspricht.
Durch Oberfächenfehler der Spiegel und des Beugungsgitters und vor allem durch die vorhandene Lichtbeugung am Eingangsspalt ist die Abbildung des Spaltes auf den Detektorelementen nicht optimal. Nicht optimal bedeutet hier eine verbreiterte Abbildung, d.h. es werden nicht 3,125 Detektorelemente überstrahlt sondern mehr. Praktisch ermittelt ist ein Wert von 4,4 Pixeln, was einer optischen Auflösung von 0,48 Ängström entspricht.
Da die Bandbreite von Etalon-Sonnenfiltern von 1Ängström bis 0,3Ängström reicht, mussten wir den Aufbau des Gitterspektrometers entsprechend anpassen. Die erste Anpassung war ein Austausch beider Spiegel gegen Spiegel mit längerer Brennweite (500mm) und dielektrischer, hochreflektiver Beschichtung. Als Zweites wurde der Eingangsspalt gegen einen schmaleren (5 Mikrometer) ausgetauscht. Der dritte Punkt war die Minimierung der vorhandenen Lichtbeugung am Spalt, die zu einer verbreiterten Abbildung auf dem Detektor führt.
Durch die längere Brennweite der beiden Spiegel verändert sich die reziproke, lineare Dispersion der Anordnung auf 0,4167nm/mm. Bei einer Detektorbreite von 29,1mm ergibt das eine maximal abbildbare Bandbreite von 12,126nm. Bei 3648 Detektorelementen folgt dann eine spektrale Bandbreite von 0,033 Ängström pro Detektorelement.
Die Spaltbreite von 5 Mikrometern ergäbe theoretisch eine ebenso grosse optische Auflösung, da die Breite eines Detektorelementes mit 8 Mikrometern grösser ist als die Spaltbreite. Durch die Minimierung der vorhandenen Lichtbeugung am Spalt konnten wir die Verbreiterung des 5 Mikrometer breiten Spaltes auf 10 Mikrometer verringern, was einer optischen Auflösung von 10/8 * 0,033 = 0,04125 Ängström entspricht.
Durch diese hohe spektrale Auflösung des Spektrometers ist es uns möglich auch Bandbreiten von sehr engen Etalon-Sonnenfiltern sicher zu messen. Bei 0,3Ängström engen Filtern erhalten wir 15 Messwerte der spektralen Durchlasskurve und können damit die Bandbreite (Halbwertsbreite FWHM, Full wide half maximum) des Sonnenfilters sicher bestimmen.
Die Banbreite des Etalon-Sonnenfilters ist nicht das einzige Qualtätskriterium für Sonnenteleskope. Auch die optische Qualität der eingesetzten Elemente ist entscheidend. In der Regel werden bei Sonnenteleskopen 3 Filter und eine Objektivlinse eingesetzt um die gewünschte Strahlung am Ausgang zu erzeugen.
Die von der Sonne eintreffende Lichtwellenfront muss also durch 4 optische Elemente und "sammelt" dabei deren optische Fehler, bevor wir die Strahlung sehen können. Ein Verfahren zur objektiven, quantitativen Bestimmung der Abbildungsgüte ist also kein "Luxus" bei der Bestimmung der Qualität von Sonnenteleskopen.
Zur Bestimmung der Abbildungsgüte bei Sonnenteleskopen setzen wir ein genormtes Testchart nach Standard USAF 1951 1X ein. Mit diesem Testchart ist es möglich die optische Auflösung von Sonnenteleskopen direkt zu bestimmen. Mit einer digitalen Aufnahme von dem um ca. 5 Grad zur Vertikalen geneigten USAF 1951 Testcharts durchs Sonnenteleskop und mit geeigneter Software sind wir in der Lage, die MTF (Modulation Transfer Function) des Sonnenteleskops sicher zu bestimmen.
Die MTF wird auch Kontrastübertragungsfunktion genannt. Sie ist die mathematische Beschreibung des Vergleiches zwischen dem Detailkontrast an Kanten eines Objektes und dem Detailkontrast deren bildlicher Darstellung. Die mathematische Beschreibung ist die Gleichung:
MTF(f) = Bildkontrast(f) / Objektkontrast(f)
wobei f die Ortsfrequenz der Modulation ist. Da es immer einen Detailkontrastverlust zwischen Objekt und Bild gibt nimmt die MTF, in Abhängigkeit der Ortsfrequenz f, Werte zwischen 1 und 0 an.
Wir bestimmen die MTF von Sonnenteleskopen nach der ISO-Norm 12233. Dort wird beschrieben, wie man die Kontrastübertragungsfunktion über das Verfahren der bildlichen, digitalen Erfassung und softwaretechnischen Auswertung einer kontrastreichen "geneigten Kante" (Slanted Edge) bestimmt.
Zur Bildaufnahme neigen wir das USAF Testchart um ca. 5 Grad zur Vertikalen und leuchten es von hinten homogen aus.
Mit einer hochauflösenden digitalen Kamera wird das Bild des Testcharts im Fokus des Sonnenteleskopes aufgenommen und zum Computer übertragen. Dort werden die kontrastreichsten, geneigten Kanten im Bild mit Hilfe der Software QuickMTF nach ISO-Norm 12233 ausgewertet.
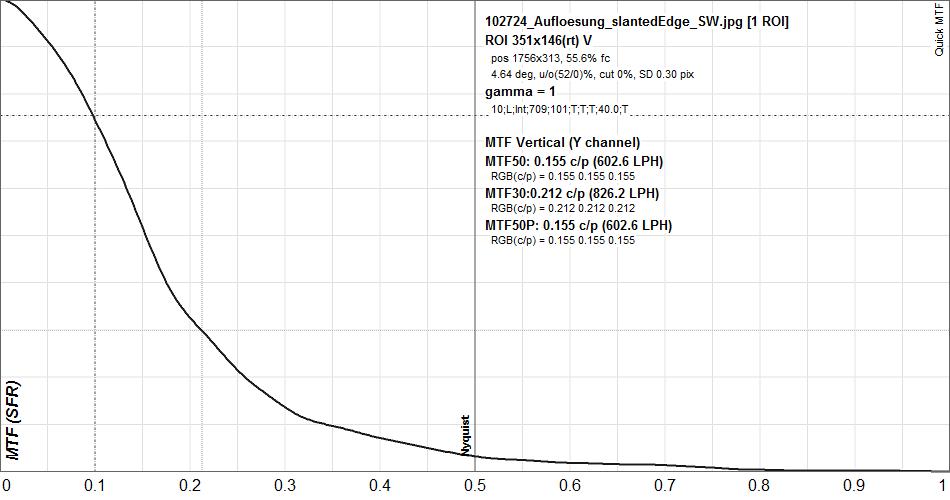
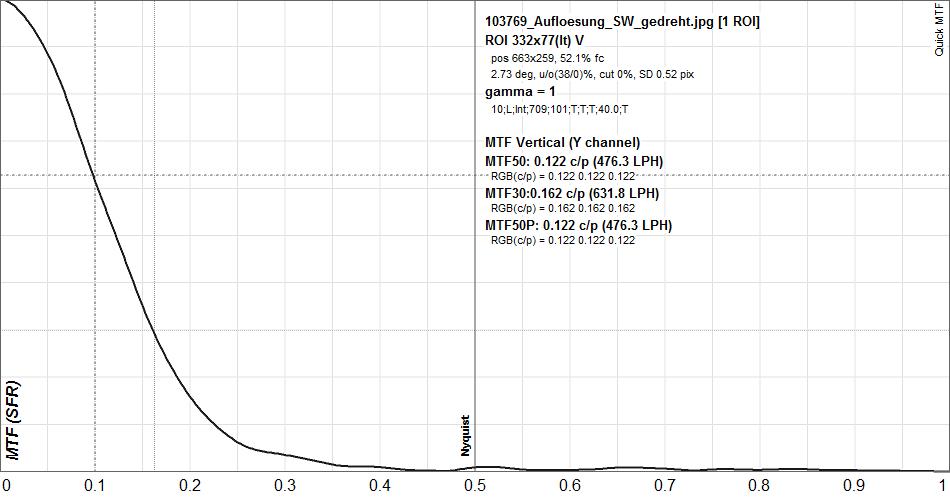
Durch die genormte Messung von Auflösung und Kontrastübertragungsfunktion ist es uns möglich, die Abbildungsgüte von Sonnenenteleskopen zu bestimmen und zu vergleichen. Als Beispiel unserer Messungen ist hier eine Auswertung unserer beiden PSTs mit den Seriennummern 102724 und 103769 beschrieben.
Die beiden folgenden Durchlasskurven wurden noch in der Originalkonfiguration des Spektrometers gemessen. Es ist zu erkennen, dass hier nicht die Bandbreite der PST-Etalons, sondern die Bandbreite des Spektrometers von damals 1,5Ängström gemessen wurde.
Die beiden Spektren wurden bei "Linksanschlag" des PST-Tuningrings gemessen. Man kannn erkennen, dass die H-alpha Linie beim linken PST nur am Rand der Durchlasskurve liegt und dadurch stark gedämpft wird. Im rechten Gerät wird die H-alpha Linie voll durchgelassen. Weiterhin kann man sehen, dass die gemessene Strahlung im linken Gerät gut doppelt so hoch ist wie die im rechten Gerät.
Die gemessenen Unterschiede sind sehr schön bei der Sonnenbeobachtung mit den Geräten zu erkennen. Im linken Gerät erscheint die Sonne bei gleicher Vergrösserung viel heller als im rechten Gerät. Oberflächenstrukturen wie die Granulation der Sonne sind im linken Gerät nur bei "Linksanschlag" des PST-Tuningrings und eher schwach zu erkennen. Im rechten Gerät erscheint die Sonne bei gleicher Vergrösserung viel dunkler und Oberflächenstrukturen sind bei "Linksanschlag" des PST-Tuningrings deutlich erkennbar.
Die beiden folgenden Bilder zeigen die Abbildungen der Gruppen 4-7 des USAF Testcharts durch die beiden PSTs. Die Abbildungsqualität des linken PSTs ist dabei sichtbar höher als die des rechten PSTs.
Die maximale Auflösung des linken PSTs liegt in Gruppe 7 zwischen Untergruppe 1 und 2. Die maximale Auflösung des rechten PSTs liegt in Gruppe 7 bei Untergruppe 1. Man kann auch erkennen, dass die Auflösung der vertikalen Streifen in beiden Geräten sichtbar geringer ist als die Auflösung der horizontalen Streifen.
Die mit Hilfe der Software QuickMTF ermittelten MTF-Kurven zeigen ebenfalls die etwas bessere Abbildungsqualität des linken Gerätes. Nimmt man üblicherweise die Ortsfrequenz bei dem der Wert der MTF auf 50% gefallen ist als Qualitätskriterium, entsprechen Werte von 0,1 einer unterdurchschnittlichen Qualität und Werte von 0,15 einer guten durchschnittlichen Abbildungsqualität.
Die Messungen an beiden Sonnenteleskopen zeigen zumindest beim PST grosse Unterschiede in der optischen Abbildung der Geräte. Die schwache Abbildung von Oberflächenstrukturen der Sonne ist definitiv nicht immer auf eine zu hohe Bandbreite des Etalons zurückzuführen, sondern auch auf die nicht korrekte Lage der Durchlasskurve, was dann zur unbeabsichtigten Dämpfung der H-alpha Linie führt.
Die Lage der Durchlasskurve kann an unseren PST-Modellen leicht korrigiert werden. Eine Korrektur am linken Gerät zeigte eine deutliche Steigerung der Erkennbarkeit von Oberflächenstrukturen. Seine guten Abbildungseigenschaften und das helle Sonnenbild machen es jetzt zu einem hervorragenden Instrument zur visuellen Beobachtung und zur Fotografie der Sonne.
Ihre Fragen zum Thema, Ihre Kritik oder Ihre Verbesserungsvorschläge können Sie gerne per Telefon oder Email an uns weitergeben.