3D-Profiler
Der von uns entwickelte, optische 3D-Profiler ist in der Lage Höhenunterschiede von glatten, reflektierenden Oberflächen im Subnanometerbereich berührungslos zu messen. Die einzelnen Komponenten sind hochwertig und gut aufeinander abgestimmt. Eine wichtige Komponente ist das Interferometerobjektiv. Wir verwenden zwei aktuelle Nikon-Objektive welche auch in den Geräten von Zygo eingesetzt werden.
Außer den beiden Nikon-Objektiven stehen noch drei Wyko-Objektive der Rx-Serie zur Verfügung, deren Vergrößerung durch passende Linsen zusätzlich angepasst werden kann. Mit den fünf Objektiven sind wir in der Lage im Vergrößerungsbereich 1,25x bis 80x zu messen, was einer lateralen (horizontalen) Auflösung von ca. 8000 Nanometern bis 200 Nanometern entspricht.
Zur Lagerung der Optik während der Messung setzen wir einen Lineartisch der Firma ASI ein. Der Tisch ist motorisiert und kann in xy- Richtung um jeweils 100mm verschoben werden, sodaß eine automatisierte Messung von Bereichen der Größe 100x100mm möglich wird. Die Steuerung der Motoren übernimmt der ASI-Controller LX4000, der selbst über die RS232 Schnittstelle per Computer angesteuert werden kann.
Der Lineartisch ist auf einer massiven Nivellierplatte befestigt, welche die genaue vertikale Ausrichtung der Optik zum Interferometerobjektiv ermöglicht. Die Kombination aus Lineartisch und Nivellierplatte steht auf einer massiven, hochwertigen Hartgesteinplatte der Firma Mahr, die dort als Unterbau für deren Oberflächenprofiler eingesetzt wird.
Die Nivellier- und Hartgesteinplatte sind zur Vermeidung von Vibrationen durch eine 15mm dicke Sorbothanmatte getrennt. Sorbothan ist ein Polymer, das sehr gute Dämpfungs- und Energieabsorptionseigenschaften besitzt. Die Sorbothanmatte verbindet die beiden Platten verschiebungssicher. Auch die zu prüfende Optik lagert während der Messung auf einer solchen Sorbothanmatte.
Die optische Baugruppe des Profilers ist auf einer identischen Hartgesteinplatte aufgebaut. Auch hier dient eine Nivellierplatte dazu die Optik vertikal genau auszurichten. Die Nivellierplatte ist aus 10mm starkem, hochfestem Aluminium. Sie kann über eine T-Nut in der Hartgesteinsplatte sicher mit dem Unterbau verschraubt werden.
Auf der Aluminiumplatte ist ein präziser Hebetisch von Newport verschraubt. Der Hebetisch ermöglicht die grobe vertikale Einstellung der Interferometeroptik zum Testobjekt. Auf dem Hebetisch sind zwei große, hochauflösende Goniometer des gleichen Herstellers verschraubt. Durch die Anordnung der Goniometer kann das Interferometerobjektiv in x- und y-Ebene gekippt werden. Das Kippen in beiden Ebenen wird benötigt, um die Interferenzstreifen zur Messung optimal einzustellen.
Auf dem oberen Goniometer ist eine Adapterplatte aus 10mm starkem, hochfestem Aluminium angebracht, die als Auflage für zwei 12mm starke Edelstahlstangen dient. Am Ende der Edelstahlstangen ist die Interferometeroptik befestigt. Die Edelstahlstangen können in Ihren Haltern um ca. 150mm verschoben werden, sodass man andere Meßstellen auf der Oberfläche des Testobjekts erreichen kann, ohne die Lage des Testobjekts zu verändern.
Um Messfehler durch Vibrationen wirksam zu unterdrücken steht der komplette Aufbau auf einer aktiv-schwingungsdämpfenden Plattform von Newport. Aktiv bedeutet, dass die 4 Schwingungsabsorber, auf denen die Plattform steht, an ein Druckluftsystem mit konstantem Druck angeschlossen sind. Ein Absorberpaar und zwei einzelne Absorber können Ihren Luftdruck, also ihre Federung, voneinander unabhängig regulieren. Durch diese Regelung können auftretende Vibrationen durch Gebäudeschwingungen, Autoverkehr, Gehen, Maschinen usw. sehr wirksam gedämpft werden.
Ausserdem wird dadurch eine aktive Nivellierung der Plattform mit Genauigkeiten im Submillimeterbereich erreicht. Laut Hersteller erreicht die Plattform bei vertikalen Vibrationsfrequenzen von 10Hz eine Dämpfung von 90%, bei horizontalen Vibrationsfrequenzen von 10Hz eine Dämpfung von 96%. Die horizontale Resonanzfrequenz der Plattform ist 3,6Hz (+10dB), die vertikale Resonanzfrequenz ist 3,2Hz (+12dB). Durch diese Eigenschaften werden die gewöhnlich in Wohngebäuden auftretenden, niederfrequenten Schwingungen (6-80Hz) sehr gut gedämpft.
Die Interferometeroptik besteht aus dem Interferometerobjektiv, das über einen Strahlteilerwürfel inline beleuchtet wird. Die Beleuchtungseinheit ist eine geregelte Halogenlichtquelle, deren Strahlung über einen 5mm starken Lichtleiter ins System eingekoppelt wird. Der Lichtstrahl wird dann auf eine Lochblende fokussiert, anschließend mit einem Achromaten kollimiert, dann über einsetzbare Filter modelliert und schließlich vor dem Strahlteiler durch eine einstellbare Irisblende im Durchmesser passend beschnitten.
Je nach Vergrößerung und Anwendung werden hochwertige Filter eingesetzt, um die Bandbreite der Beleuchtung anzupassen. Der Strahlteilerwürfel ist in einem Optikhalter befestigt der in x- und y-Ebene verkippt werden kann. Am oberen Teil des Optikhalters ist der Tubus der Kamera befestigt. Durch Einstellungen am Optikhalter kann so die Bildebene der Kamera optimal auf den Strahlengang des Interferometerobjektivs eingestellt werden.
Für die auf unendlich korrigierten Nikon-Objektive wird im Kameratubus zusätzlich eine passende Tubuslinse integriert, die Bildfehler der Objektive wirksam korrigiert und das Objektivbild auf den Kamera-Sensor fokussiert. Als Bildsensor setzen wir eine monochrome 1,3MP CMOS-Kamera des Herstellers Point Grey ein. Die Kamera schafft bei einer Auflösung von 1280x1024 Bildpunkten eine Framerate von 150FPS und wird über eine eigene USB3.0/PCI-Steckkarte mit dem Computer verbunden. Diese Eigenschaften ermöglichen es, große Datenmengen schnell und sicher zur Weiterverarbeitung zum Computer zu übertragen.
Eine weitere wichtige Komponente zum Aufbau des 3D-Profilers ist eine Vorrichtung zur Bewegung des Interferometerobjektivs in der Vertikalen. Die Bewegung soll dabei so linear wie möglich sein. Die Bewegungslängen liegen im Nanometerbereich und sollen sehr schnell und präzise erfolgen. Diese Anforderungen werden sehr gut von Piezoelementen erfüllt. Wir verwenden dazu eine Piezobühne vom Hersteller PI.
Das Piezoelement verbiegt bei einer solchen Bühne Festkörpergelenke, die eine sehr lineare Bewegung in vorgegebener Richtung ermöglichen. Die Piezobühne legt im Spannungsbereich -20V bis 120V eine Strecke von ca. 120 Mikrometern zurück. Das Interferometerobjektiv wird über einen Haltering direkt mit der Piezobühne verschraubt. Über zusätzliche Sicherungsringe wird ein möglicher Sturz des Objektivs auf die Testoptik verhindert.
Um die hohen Spannungen zum Betrieb der Piezobühne zu erzeugen, wird ein analoger Piezoverstärker des Herstellers Piezomechanik eingesetzt. Der Verstärker ermöglicht die stufenlose Regelung der Verstärkung des Eingangssignals, sowie die stufenlose Einstellung einer Offsetspannung über den gesamten Spannungsbereich.
Da die Auflösung eines Piezoelementes nur durch das Rauschen der angelegten Spannung begrenzt wird, ist ein niedriges Verstärkerrauschen sehr wichtig. Das Rauschen des eingesetzten Verstärkers wird vom Hersteller mit 0,3mV angegeben. Eine Spannung von 0,3mV erzeugt also eine Bewegung der eingesetzten Piezobühne von: 120000nm/140000mV = 0,86nm/mV, also für 0,3mV Spannung eine Bewegung von ca. 0,26 Nanometern. Für das eingesetzte Messverfahren ist diese Auflösung vollkommen ausreichend.
Für berührungslose, optische 3D-Profiler mit dem beschriebenen Aufbau existieren zwei unterschiedliche Messtechniken. Die Phase-Shifting-Interferometry (PSI) und die Vertikal-Scanning-Interferometry (VSI). Beide Techniken können mit derselben Hardware eingesetzt werden. PSI wird bei glatten Oberflächen eingesetzt, die keine abrupten Sprünge oder sogar Stufen aufweisen.
VSI kann auch für rauhe Oberflächen mit Stufen eingesetzt werden. PSI erzielt bei glatten Oberflächen eine wesentlich höhere Auflösung las VSI. Da die Flächen von optischen Bauteilen sehr glatt und meistens auch recht eben sind, setzen wir die Phase-Shifting-Interferometry ein.
Allerdings ist für die Zukunft geplant den 3D-Profiler zusätzlich mit VSI auszustatten, um auch stark gekrümmte, optische Oberflächen gut vermessen zu können. Für VSI ist eine grössere Bandbreite der Beleuchtungswellenlänge nötig, was andere Filter in der Beleuchtungseinheit erfordert. Die grössere Anpassung ist allerdings bei der Auswerte-/Steuersoftware nötig.
Bei Phase-Shifting-Interferometry macht man sich die Tatsache zu nutze, dass die Phasenverschiebung im Interferogramm linear von der Höhe der gemessenen Oberfläche abhängt. Der Zusammenhang ist: h = lambda/(4*PI) * phi, wobei "phi" der Winkel der Phaseverschiebung im Bogenmass und "lambda" die mittlere Wellenlänge der Beleuchtung ist. Die mittlere Wellenlänge der Beleuchtung kennt man durch die eingesetzten Filter. Kann man die Phase phi bestimmen, dann kann man die Höhe der Oberfläche über die obige Gleichung leicht errechnen.
Zur Bestimmung der Phasenverschiebung nimmt man, bei verschiedenen Höhen des Interferometerobjektivs über der zu messenden Spiegeloberfläche, monochrome Bilder der entstehenden Interferogramme auf. Die Bilder werden von der Kamera zum Computer übertragen und dort mit Software ausgewertet.
Ausgewertet werden die Intensitätswerte für jedes einzelne Bildpixel in den aufeinanderfolgenden Bildern, d.h. hat man 5 Bilder aufgenommen, existieren für jedes Pixel fünf Intensitätswerte. Diese Intensitätswerte werden nun über bereits existierende Algorithmen (mathematische Gleichungen) miteinander verknüpft. Das Ergebnis der Rechnung ist die Phasenverschiebung für dieses Pixel, d.h. man kann durch die Messung von Pixelintensitäten die Höhe eines Punktes auf der Oberfläche genau messen!
Da wir die Software zur Auswertung der Interferogramme selbst entwickeln, können wir auch bestimmen, welche Algorithmen wir zur Auswertung benutzen. Zur Bestimmung der Phasenverschiebung aus den Intensitätswerten der Bildpixel benutzen wir einen 5-Frame Algorithmus der von Schwider und Hariharan entwickelt wurde.
5-Frames bedeutet, dass 5 Interferogrammbilder aufgenommen werden. Der Verfahrweg des Interferometerobjektivs zwischen den einzelnen Bildaufnahmen beträgt beim Schwider-Hariharan Algorithmus PI/2. Bei einer mittleren Wellenlänge der Beleuchtung von 660nm entsprechen PI/2 einem Viertel der Wellenlänge, d.h. 165nm optischer Weg.
Weil der optische Weg des Lichts doppelt so groß ist wie die Verschiebung des Interferometerobjektivs, muss das Interferometerobjektiv also zwischen der Aufnahme von 2 Frames 82,5nm weit verschoben werden. Diese Verschiebung wird über die Größe der angelegten Spannung am Ausgang des Piezoverstärkers, sowie über die einzustellende Framerate der Kamera geregelt.
Framerate sowie Piezospannung steuern bzw. erzeugen wir über unsere Auswerte-/Steuersoftware. Bei der Framerate von 30 Bildern pro Sekunde und einer mittleren Wellenlänge der Beleuchtung von 660nm muss die Piezobühne das Interferometerobjektiv also bei 5 aufzunehmenden Bildern linear um 330 Nanometer in 167 Millisekunden verschieben.
Die Ausgangspannung des Piezoverstärkers muß also eine Spannungrampe sein, die ihren Spannungwert in 167 Millisekunden von 0 auf 384 Millivolt ändert. Berücksichtigen wir einen Verstärkungsfaktor des Piezoverstärkers von 5 ergibt sich eine Eingangsspannung am Piezoverstärker linear von 0 auf 76,8 Millivolt in 167 Millisekunden.
Um eine Spannung dieser Form durch einen Computer erzeugen zu können, benötigt man einen Digital-Analog-Wandler. Das von uns eingesetzte Gerät ist eine USB-Version vom Hersteller Adlink mit zwei analogen Ausgängen mit je 16-Bit Auflösung und 1Ms/s Datenübertragung. Das Gerät wird über unsere Auswerte-/Steuersoftware angesteuert.
Algorithmen wie der 5 Frame Schwider-Hariharan unterscheiden sich durch die Anfälligkeit gegenüber Fehlern, die beim Messen mit optischen 3D-Profilern auftreten. Bedeutende Fehler sind z.b. Vibrationen, Phasenfehler durch nichtlineare Bewegungen (Hysteresekurve Piezo) und nichtlinearitäten in den Kamerasensoren. Der eingesetzte Algorithmus ist recht unempfindlich gegenüber diesen Fehlerquellen.
Da in unserem Messraum vergleichsweise gute Umgebungsbedingungen für solch empfindliche Messungen herrschen, brauchen wir nicht auf Algorithmen zurückzugreifen, die einen Fehler besser tolerieren aber dafür gegenüber anderen Fehlern empfindlicher sind.
Um die Genauigkeit unserer Messungen noch zu steigern, setzen wir den 5 Frame Schwider-Hariharan in einer sogenannten Averaging-Version mit 3-Buckets ein, d.h. anstatt 5 Frames nehmen wir 7 Frames auf und bilden aus diesen Frames 3x5-Frame-Messungen, deren Ergebnisse dann in der Auswertesoftware gemittelt werden.
Durch eine solche Mittelung werden Fehler durch ungleiches Phasenschieben in den einzelnen PI/2-Intervallen ausgeglichen. Die Steigerung der Phasengenauigkeit durch diese Maßnahme ist enorm. Erklärung Averaging Version mit 3-Buckets: Vorhandene Frames: 1,2,3,4,5,6,7 daraus wird: Bucket 1 = 1,2,3,4,5 Bucket 2 = 2,3,4,5,6 und Bucket 3 = 3,4,5,6,7
Der Winkel der Phasenverschiebung im Bogenmass wird also durch die Funktionsgleichung des Schwider-Hariharan-Algorithmus berechnet. Diese Funktionsgleichung ist allerdings eine Arkustangensfunktion die nur im Winkelbereich von -PI/2 bis +PI/2 definiert ist. Um das Ergebnis im gesammten Winkelbereich von -PI bis +PI oder 0 bis 2*PI zu erhalten, muss man das Ergebnis noch transformieren.
Zu diesem Zweck wertet man entweder die Vorzeichen von Zähler und Nenner der Arkustangesfunktion aus oder benutzt einfach die atan2-Funktion, welche in den gängigen Programmiersprachen schon existiert. Das Ergebnis dieser Rechnung ist dann der Winkel der Phasenverschiebung im Bogenmass im Bereich von 0 bis 2*PI.
Da dieser Winkel sich allerdings mit einer Periode von 2*PI wiederholt sind die Ergebnisse der bisherigen Rechnung noch nicht eindeutig. Zum besseren Verständnis: Errechnet man für ein Pixel eine Phase von 2*PI und für ein benachbartes Pixel eine Phase von PI, weiß man nicht ob die "absolute Phasenlage" des zweiten Pixels vom ersten Pixel aus gesehen 3*PI (=2*PI+PI) oder PI (=2*PI-PI) ist.
Der nächste Lösungsschritt ist also das Ermitteln der "absoluten Phasenlage" aller Pixel. Dazu benutzt man sogenannte Phase-Unwrapping-Algorithmen, was auf deutsch ungefähr ein "Aufwickeln" der Phase bedeutet. Beim Phase-Unwrapping wird von einem Pixel ausgehend immer ein Nachbarpixel bearbeitet, d.h. man errechnet aus der "absoluten Phasenlage" des vorausgehenden Pixels und zwei Annahmen die absolute Phasenlage des folgenden Pixels.
Die beiden Annahmen sind dabei das Einhalten der Nyquist-Bedingung und die Annahme, dass sich die Phasenlage zwischen zwei benachbarten Pixeln um nicht mehr als PI ändert. Das Einhalten der Nyquist-Bedingung führt zu einer Überprüfung/Anpassung der Pixelauflösung des Kamerasensors für jede Vergrößerung des Interferometerobjektivs in Abhängigkeit von der mittleren Wellenlänge der verwendeten Beleuchtung.
Das Eingrenzen der Phasenänderung auf PI zwischen zwei benachbarten Pixeln führt zu der eingeschränkten Verwendbarkeit der Phase-Shifting-Interferometry nur für glatte Oberflächen. Allerdings machen diese beiden Annahmen ein Phase-Unwrapping und somit die Verwendbarkeit dieser hochauflösenden Technik erst möglich.
Die Abhängigkeit der Phasenlage eines Pixel von der des vorherigen Pixel macht das Phase-Unwrapping sehr fehleranfällig. Ist die vorher berechnete Phasenlage falsch, werden alle nachfolgenden Pixel falsch berechnet. Passiert der Fehler am Anfang der Kette ist das komplette Bild der Oberfläche falsch.
Es gilt also, solche fehlerhaften Pixel oder auch sogenannte schlechte Pixel vorher zu bestimmen und vom Phase-Unwrapping auszuschliessen. Schlechte Pixel sind solche, die eine niedrige Modulation ihrer Intensitätswerte aufweisen, d.h. wandern die Interferenzstreifen durch die Verschiebung des Interferometerobjektives über die Oberfläche der Testoptik, wird ein Pixel während der Aufnahme eines kompletten Framesets bei einer Phasenverschiebung von PI/2 zwischen den Frames, einmal abgedunkelt und einmal ausgeleuchtet.
Diesen Intensitätsunterschied nennt man die Modulation des Pixels. Bei richtig eingestellten Kameraparametern und guter Beleuchtung liegt die Modulation der guten Pixel zwischen 70% und 85% Intensitätsunterschied. Um schlechte Pixel von der weiteren Verarbeitung auszuschliessen, bestimmt man vor dem Phase-Unwrapping die Modulation aller Pixel und kennzeichnet die schlechten Pixel.
Im Laufe der Zeit wurden sehr viele unterschiedliche Techniken für das Phase-Unwrapping entwickelt. Einen guten Überblick dieser Techniken erhält man in dem Buch "Two-Dimensional Phase Unwrapping: Theory, Algorithms, and Software" von Dennis C. Ghiglia und Mark D. Pritt.
Der von uns benutzte Algorithmus ist ein zweidimensionaler, quality-guided Algorithmus mit der Möglichkeit Pixel zu maskieren und somit vom Phase-Unwrapping auszuschliessen. Zweidimensional bedeutet, dass der "Unwrapping-Pfad" nicht zeilenweise oder spaltenweise abgearbeitet wird, sondern in alle Richtungen der zweidimensionalen Ebene führen kann.
Quality-guided bedeutet, es werden gezielt Pixel mit hoher Qualität gesucht um das Phase-Unwrapping durchzuführen. Erst wenn alle Pixel hoher Qualität bearbeitet wurden, werden Pixel mit geringerer Qualität bearbeitet. Die Qualität der Pixel wird vom Unwrapping-Algorithmus mit bestimmten Techniken ermittelt und in der sogenannten Quality-Map gespeichert, die dann beim Unwrapping-Prozess zur Auswahl der Pixel benutzt wird.
Im von uns benutzten Umwrapping-Algorithmus wird die "Phase Derivative Variance Technik" verwendet, um die Quality-Map zu erzeugen. Diese Technik benutzt Pixelbereiche einer bestimmten Größe n x n und berechnet die (Wrapped-) Phasendifferenzen der enthaltenen Pixel um die Qualität zu bestimmen. Ein großer Unterschied der lokalen Phasendifferenzen bedeutet eine schlechte Qualität des Pixelbereichs, da solche lokalen Unterschiede auf fehlerhafte Phasensprünge oder grosses Rauschen der Pixelintensitäten hindeutet.
Der von uns implementierte Algorithmus wird im angegebenen Buch sehr gut beschrieben und auch mit schon fertigen Code-Teilen zur Unterstützung bei eigenen Softwareprojekten vorgestellt. Nach dem Phase-Unwrapping liegt dann ein Phasenbild der Oberflächenstruktur vor. Dieses Phasenbild wird nun über den oben beschriebenen, linearen Zusammenhang zwischen Phasenverschiebung und Höhenunterschied "h = lambda/(4*PI) * phi" berechnet. So erhält man eine hochaufgelöste Höhenkarte der Oberflächenstruktur, die nun softwaretechnisch weiterverarbeitet werden kann.
Wie aus der bisherigen Beschreibung des Datenverarbeitungsvorgangs ersichtlich, ist die digitale Bildverarbeitung ein fundamentaler Bestandteil der Phase-Shifting- Interferometry. Wir benutzen zur digitalen Bildverarbeitung die Softwarebibliothek OpenCV. OpenCV ist eine mächtige Sammlung von Bildverarbeitungsfunktionen, die als Open-Source-Software verfügbar ist und deren Code in eigene Softwareprojekte eingebunden werden darf.
Zur Entwicklung unserer Programme benutzen wir eine aktuelle Version von Microsofts Visual Studio in Verbindung mit der Programmiersprache Visual C++. Da OpenCV ebenfalls in C/C++ Code geschrieben ist, können die verwendeten Codeteile zur digitalen Bildverarbeitung sehr gut in unsere Software integriert werden.
Die berechnete Höhenkarte der Oberflächenstruktur kann jetzt mit einigen Programmoptionen weiterverarbeitet werden. Optionen sind zum Beispiel das Entfernen der Form der Oberfläche (sphärisch oder parabolisch) oder das Ausrichten einer planen Oberfläche. Die Software bietet auch einen automatisierten Ausschluss von "Ausreissern" für die weitere Verarbeitung der Daten. RMS- und PV-Werte Oberflächenbildes werden automatisch berechnet und in Textdateien abgespeichert.
Bisher haben wir, in Abhängigkeit von der Vergrösserung des Interferometerobjektives, nur einen kleinen, rechteckigen Teil der Oberfläche unseres Testobjekts ausgewertet. Die ausgewertete Fläche ist rechteckig, weil die beleuchteten, digitalen Kamerasensoren in der Regel rechteckig sind. Die benutzte Kamera hat zum Beispiel bei einer Auflösung von 1280 x 960 Pixeln und der angegebenen Pixelgröße von 4,8 Mikrometern eine Sensorfläche von 6,14mm x 4,61mm.
Setzen wir das Nikon Interferometerobjektiv mit 5-facher Vergrößerung ein, ergibt sich eine auswertbare Bildfläche von 1,23mm x 0,92mm. Möchten wir nun die maximalen Verfahrwege unserer xy-Bühne von 100mm x 100mm nutzen, also eine Oberfläche von 100mm x 100mm automatisiert auswerten, müssen wir 8837 Bilder, wie oben beschrieben erzeugen, und zu einer zusammenhängenden Oberfläche zusammenführen.
Da beim Zusammenführen (Stitching) der einzelnen Bilder eine Überlappung von ca. 20% der Bildgrösse erforderlich ist, müssen wir sogar 13808 Oberflächenbilder erzeugen. Bei der Bildgrösse von 1280 x 960 Pixeln und der Auflösung von 8-Bit ergäbe das eine unkomprimierte Datenmenge von 137GigaByte. Kalkuliert man jetzt noch ein, dass 7 Frames (Bilder) benötigt werden, um ein Oberflächenbild zu erzeugen, werden dann unkomprimierte 950 GigaByte an Daten für eine Messung zum Computer übertragen und verarbeitet.
Um solche Datenmengen in praktikablen Zeiträumen verarbeiten zu können, ist eine schnelle Hardware und effiziente Verarbeitungsalgorithmen erforderlich. Aus den genannten Gründen werden bei Phase-Shifting-Interferometry, insbesondere bei hohen Vergrösserungen, meist kleinere Oberflächenbereiche ausgewertet.
Zum Zusammenfügen (Stitching) der vielen Einzelbilder setzen wir das Programm "ImageJ" ein. ImageJ ist wie OpenCV frei erhältliche Software deren Code in eigenen Softwareprojekten verwendet werden darf. Allerdings ist ImageJ im Gegenteil zu OpenCV auch ein eigenständiges Programm, dass für die automatisierte Verarbeitung von Mikroskopbildern im wissenschaftlichen Bereich eingesetzt wird. Die Software besitzt dazu eine Reihe sehr guter Stitching-Module, mit denen das Zusammenführen der Einzelbilder gut möglich ist. Zum Stitchen benutzen wir ImageJ unabhängig von unserer Software.
Zur Steuerung der ASI-Bühne während des Programmlaufs verwenden wir die frei erhältliche Software "MicroManager". MicroManager wurde entwickelt um motorische xy-Bühnen und andere Hardware von kommerziellen Mikroskopen zu steuern. Mittlerweile gibt es sehr gute Module für die meisten erhältlichen, wissenschaftlichen Mikroskope.
Zusammen mit ImageJ, das auch mit dem MicroManager ausgeliefert wird, erhält man eine mächtige Software für die automatisierte Bildaufnahme und Bildverarbeitung von Mikroskopen. Das MicroMangager-Modul für die ASI-Bühne wird aus unserer Software heraus, über vorhandene Programmierschnittstellen, angesteuert und gibt uns die Möglichkeit, die ASI-Bühne während des Programmlaufs zu steuern.
Sind die einzelnen Oberflächenbilder zusammengeführt, kann das entstandene Bild der Oberflächenstruktur softwaretechnisch weiter ausgewertet werden. Dazu benutzen wir die OpenSource Software "Gwiddion". Gwiddion ist ebenfalls frei verfügbar und wurde zur Analyse von Datendateien aus SPM/AFM-Geräten sowie optischen Profilern entwickelt.
Die Software besitzt unter anderem Funktionen zur Bestimmung von in der ISO definierten Rauheitsparameter, Funktionen zur Fehlerkorrektur von typischen, bei den angewandten Techniken auftretenden Oberflächenartefakten, oder zur Maskierung von bestimmten Bereichen.
Gwiddion stellt notwendige Filterfunktionen (auch 1D-FFT und 2D-FFT Filter) zur Verfügung und beherrscht integrale Transformationen wie 2D FFT, 2D continuous wavelet transform (CWT), 2D discrete wavelet transform (DWT), wavelet anisotropy detection und radial FFT profile. Ausserdem stellt das Programm eine 3D-Ansicht der Oberflächen zur Verfügung, die sehr schön an eigene Bedürfnisse anpassbar ist.
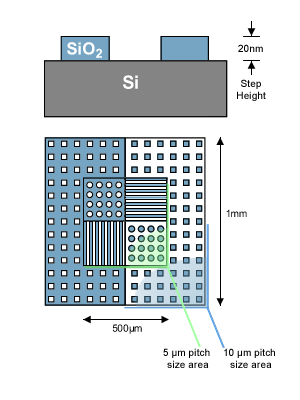
Der 3D-Profiler wird vor jeder Messung kalibriert. Dazu verwenden wir einen Standard aus Silizium, auf dem Felder mit Strukturen aus Siliziumdioxid mit einer Höhe von ca. 20 Nanometern aufgebracht sind. Die genaue Höhe der Strukturen ist rückführbar, sie wird nach der Herstellung des Standards vermessen und ist auf dem mitgelieferten Datenblatt angegeben.
Da die Strukturen des Standards auch in lateraler (horizontaler) Richtung sehr genaue, rückführbare Abstände haben, kann man die Felder auch zum Kalibrieren der horizontalen Auflösung des 3D-Profilers verwenden.
Ein Bild des Aufbaus vom Standard im Herstellerdatenblatt:
Zwei Oberflächenbilder dieses Standards vermessen mit dem 3D-Profiler:
Als Interferometerobjektiv wurde bei der Bildaufnahme das Nikon-Mirauobjektiv mit 20facher Vergrösserung eingesetzt. Die Pixelgrösse der Originalbilder ist 1280x960 Pixel und die Bildgrösse ist 320x240 Mikrometer. Die Bilder sind originalbelassen, d.h. es wurden noch keine Filter oder sonstige Werkzeuge eingesetzt. Die grösseren Strukturen haben Abstände von 10 Mikrometern, die kleineren Strukturen haben Abstände von 5 Mikrometern.
So ... bei allen interessierten Lesern, die es bis hierher geschafft haben, möchte ich mich recht herzlich für die Aufmerksamkeit bedanken! Sicherlich wirft diese grobe Beschreibung unserer Messmöglichkeiten und der am 3D-Profiler eingesetzten Techniken einige Fragen auf. Sie werden hiermit ausdrücklich dazu aufgefordert Ihre Fragen, Ihre Kritik oder Ihre Verbesserungsvorschläge an uns per Telefon oder Email weiterzugeben.


